PDF Version:
This training lab is an introduction to modelling planning problems using the Planning Domain Definition Language (PDDL). By following this tutorial you will learn the basics of PDDL, create a model for temporal logistics, and generate plans using an online solver.
The training lab will consist of an asynchronous tutorial (this document) and an online session:
- You have one week to follow this tutorial and complete the exercises in your own time. Please discuss solutions and error messages on the school’s #slack channel.
- During the online session there will be:
- an introduction to the components of a PDDL planning task (Lab PS-1)
- a Q&A session (Lab PS-2)
- a work-through of the model solution to the final exercise (Lab PS-3)
Tools and software required:
- Everything can be run online using http://editor.planning.domains
Other resources (not required if using online editor):
- The TFD temporal planning system: http://gki.informatik.uni-freiburg.de/tools/tfd
- The POPF temporal planner: https://nms.kcl.ac.uk/planning/software/popf.html
Other references:
- The PDDL wiki, which includes a reference and guide: https://planning.wiki
- An Introduction to the Planning Domain Definition Language.
Haslum, P., Lipovetzky, N., Magazzeni, D., Muise, C., (2019). - PDDL – The Planning Domain Definition Language.
Ghallab, M., Knoblock, C., Wilkins, D., Barrett, A., Christianson, D., Friedman, M., Kwok, C., Golden, K., Penberthy, S., Smith, D., Sun, Y., & Weld, D. (1998). - Fox, M., & Long, D. (2003). PDDL2.1: An Extension to PDDL for Expressing Temporal Planning Domains. CoRR, abs/1106.4561. http://arxiv.org/abs/1106.4561
Outline
- The Online Editor
- Simple Switches
- Basic Logistics
- Temporal & Numeric Logistics
The Online Editor
For this tutorial, we will use the online PDDL editor at planning.domains:
- http://editor.planning.domains
Feel free to use an offline editor and planner of your choice instead. Two such planners are linked from the other resources list at the top of the tutorial.
Sessions
The online editor allows you to save and share sessions. This is a useful way to work together, or to share read-only copies of your work when asking for help or giving examples.
- Saving a Read only session will not affect the original session.
- Saving a Read/Write session will overwrite the session with your current workspace.
Be careful to share the correct link!
Simple Switches
Task: create a planning model that executes a set of simple actions to toggle switches.
Remember to make use of the school’s #slack channel and to make note of problems and questions you want to ask during the online session.
The main components of a planning problem are:
- A set of things that make up the world (the objects)
- The properties that are used to describe the state of those things (the predicates)
- A description of how the world behaves and the capabilities of the agent (the actions)
- A description of the initial situation (the initial state)
- A description of the desired situation (the goal)
Initial Template
http://editor.planning.domains/#read_session=jfespcjFc3
Using the link above take a look at the domain and problem PDDL files in the editor. Note that the predicates and actions are described in the domain file. The objects, their initial situation, and the goal are described in the problem file.
There are example solution links for exercises 2.1 and 2.2- but there will be more than one way to model this problem, and your solution may differ!
Exercise 2.1 More switches
Extend the domain and problem so they describe the following scenario:
- There are three switches, all initially off.
- Switches can be turned on and off again.
- The goal is to turn all three switches on.
Example Solution link: http://editor.planning.domains/#read_session=iseLBtK6jo
Exercise 2.2 Tricky Switches
Update the problem so that:
- There are five switches.
- A switch can only be switched on if it has a neighbour that is already on.
- The five switches are in a row so that each switch has two neighbours, except the two at the ends of the row which only have one.
- The five switches are in initial positions: {off, off, on, off, off}.
You may have to create a new predicate to describe that two switches are neighbours. For example:
(neighbours ?s1 ?s2 - switch)Example Solution Link: http://editor.planning.domains/#read_session=ob1iWAQRpt
Exercise 2.2 Trickier Switches (bonus challenge)
Update the problem so that:
- There are ten switches in a row.
- The ten switches are in initial positions: {on, off, on, off, off, on, off, off, on, off}.
- A switch can only be switched on if it has exactly one neighbour that is already on.
Basic Logistics
Task: create a planning model for the basic logistics task in which drivers use trucks to deliver packages.
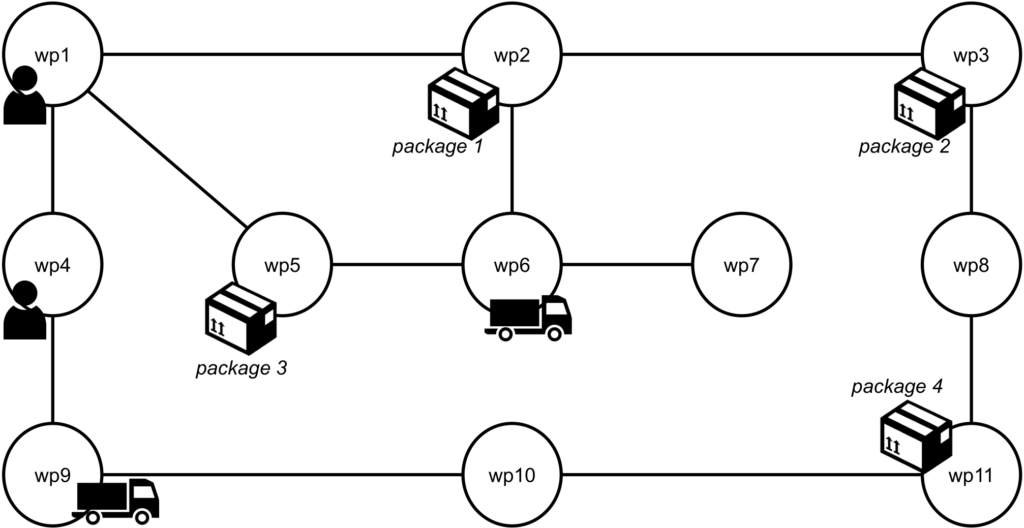
The diagram above describes a set of locations and paths.
Exercise 3.1 Initial Domain and Problem
Domain
You must write the domain file. The domain file should include a list of predicates and actions. It can optionally include a list of types.
The actions should allow for the following activities:
- Packages can be loaded into and out of trucks (a driver does not have to be present).
- Drivers can walk between connected locations.
- Drivers can get into and out of trucks.
- A truck with a driver inside can move between connected locations.
The list of predicates should be those sufficient to support the actions.
Everything not explicitly stated is up to you. For example, you can decide if it is possible for more than one driver to ride in the same truck.
Problem
You must also write the problem file. The problem file will need to include a list of objects, an initial state, and a goal.
The objects might be:
- Two drivers
- Two trucks
- Four packages
- Eleven locations
However, your domain description may be written so that a different set of objects can be used to fulfil the same required activities.
The initial state is shown in the diagram above:
- The drivers are in locations {wp1, wp4}
- The trucks are in locations {wp6, wp9}
- The packages are in locations {wp2, wp3, wp5, wp11}
The goal:
- Both drivers must be home in wp1.
- The packages must be in their destination locations:
- package 1 and 3 in location wp9
- package 2 and 4 in location wp2
Online Editor Plugins
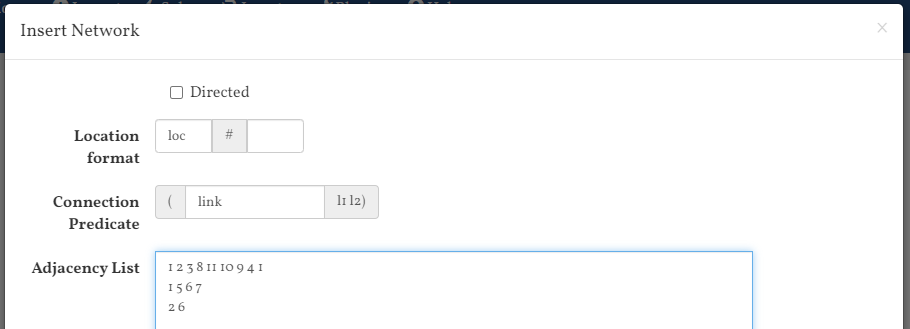
If you are using the online editor, you can describe the connectivity of the locations using a plugin. This is a very handy way to generate many propositions in the initial state without having to type them by hand!
First go to Plugins and install Misc PDDL Generators:

Second, choose insert->network and enter the adjacency list describing the network.
Example Solution Link
Part 4 will build upon the solution to Part 3. Feel free to continue to build upon your own solution or to use the example solution.
http://editor.planning.domains/#read_session=2JDdMRo8iW
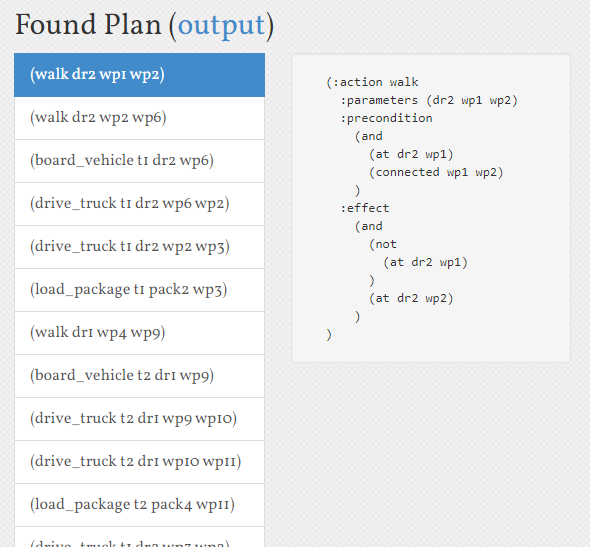
Our plan looked like this:
Temporal & Numeric Logistics
Task: Up until now we model time as a sequence of states and actions are instantaneous. In this section we’re going to update the problem to include functions, durative actions, and deadlines.
- Functions describe numeric properties, such as the length of connections.
- Durative actions model actions that take time to execute, and can be executed concurrently with other actions.
- Deadlines will be added on the delivery time of packages.
Functions
Functions describe real-valued numeric properties. They are defined like predicates in the domain file. For example:
(:functions
(fuel-level ?v - vehicle)- Comparisons between numeric expressions can be used as Boolean values:
(>= (fuel) (∗ (distance ?from ?to) (fuel_consumption)))- Effects can modify functions by numeric expressions:
(and
(assign (speed) 0)
(increase (distance_travelled) (distance ?from ?to))
(decrease (fuel) (∗ (distance ?from ?to) (fuel_consumption)))
)Below is an example initial state that assigns initial values to functions:
(:init
(at truck Rome)
(at car Paris)
(= (fuel-level truck) 100)
(= (fuel-level car) 100)
)Durative Actions
A durative action is defined differently from an instantaneous action.
(:durative-action attend_lecture
:parameters (?s - student ?l - lecturer ?r - room)
:duration (<= ?duration 120)
:condition (and
(at start (awake ?s))
(at start (in ?l ?r))
(at start (in ?s ?r))
(over all (awake ?l)))
:effect (and
(at end (not (awake ?s)))))- The
:durative-actiondeclaration is used instead of:action. - A
:durationconstraint expresses the time taken to perform the action. The planner is free to choose any duration that complies with the duration constraint. - The
:preconditionis replaced by a:conditionthat includes: - at start conditions, which must be true in the state that the action is applied.
- at end conditions, which must be true in the state that the actions is completed.
- over all conditions, which must be true throughout the duration of the action.
- Effects that can also be at start or at end.
Exercise 4.1 Durative Actions
Convert the actions of the logistics problem to be durative. The following solution link includes temporal plugins. Either start from this template, or open this link and replace the domain and problem with your own solution from Part 3.
http://editor.planning.domains/#read_session=JAlHoWLhP2
The temporal plugins include a temporal planner to solve the problems, and a timeline vizualiser:
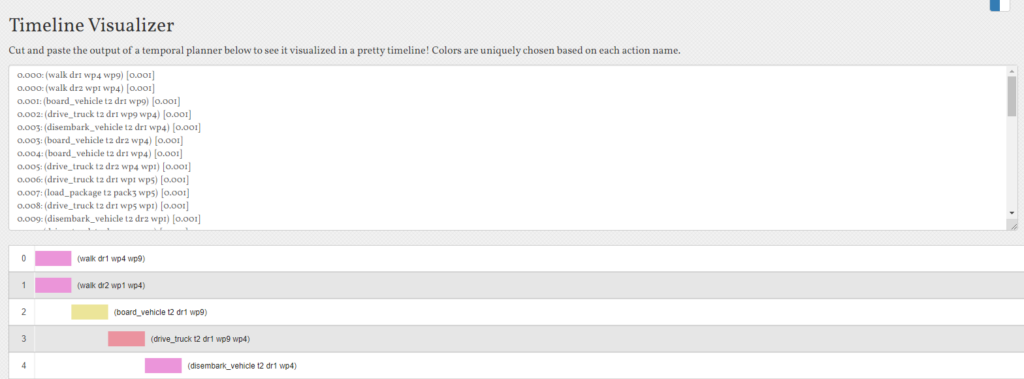
The durative actions in the domain should model the following details:
- Packages can be loaded into and unloaded from trucks (10 time units).
- Drivers can walk between connected waypoints (at a speed of 0.5).
- Drivers can get into and out of trucks (10 time units).
- Trucks with drivers can drive between connected waypoints (at a speed of 1).
The distances of each connection are shown below:
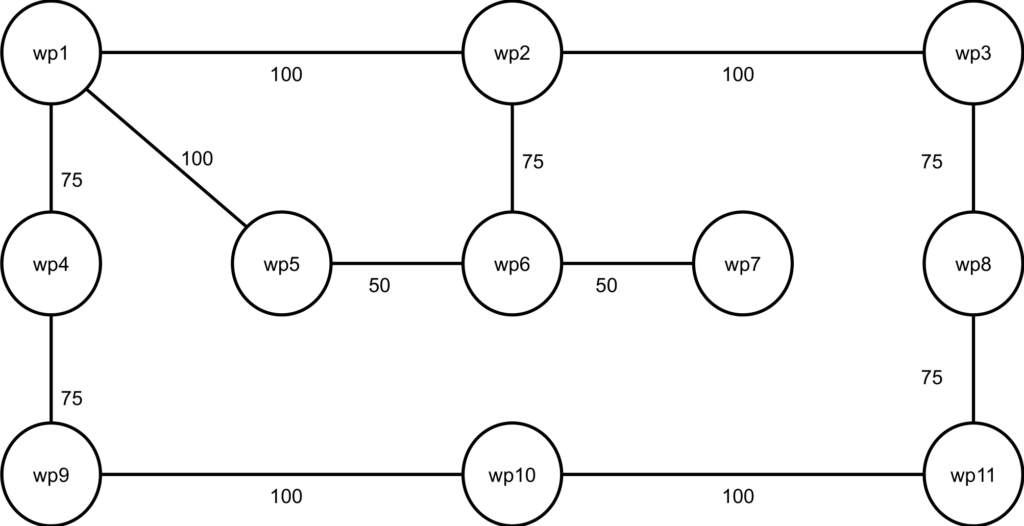
Tip: if the planner is unable to find solutions to the problem, try using a much smaller problem instance until you are confident the domain is correct.
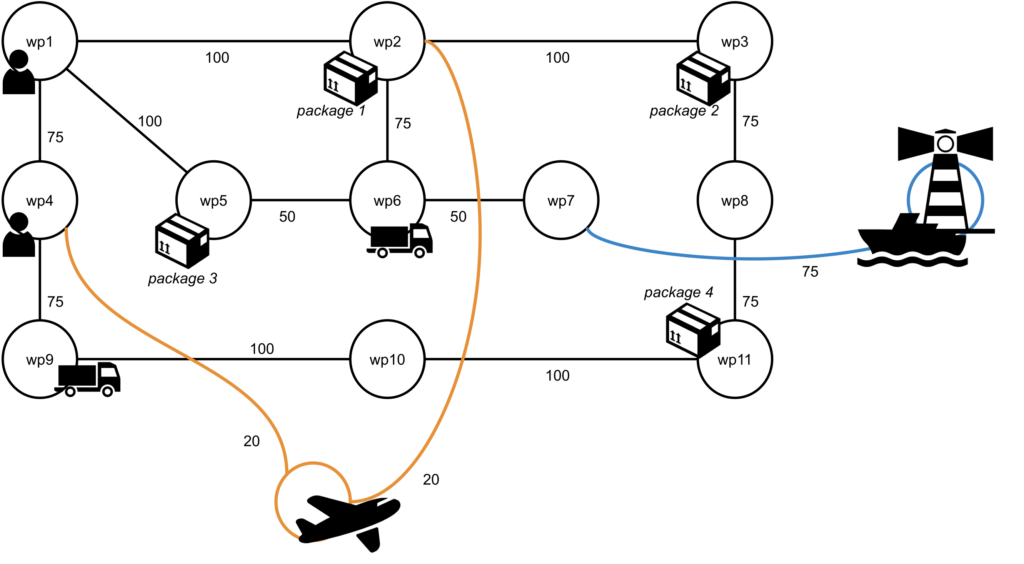
Exercise 4.2 Planes and Boats
Extend the problem to include both planes and boats.
- The boat and the plane don’t need drivers to move.
- They can only travel over the blue and yellow edges (connected to the lighthouse and the sky). Trucks can only travel on roads.
- The boat travels at a speed of 1.5.
- The plane travels at a speed of 2.
The new connections, locations, and the initial state of the plane and boat are shown below.
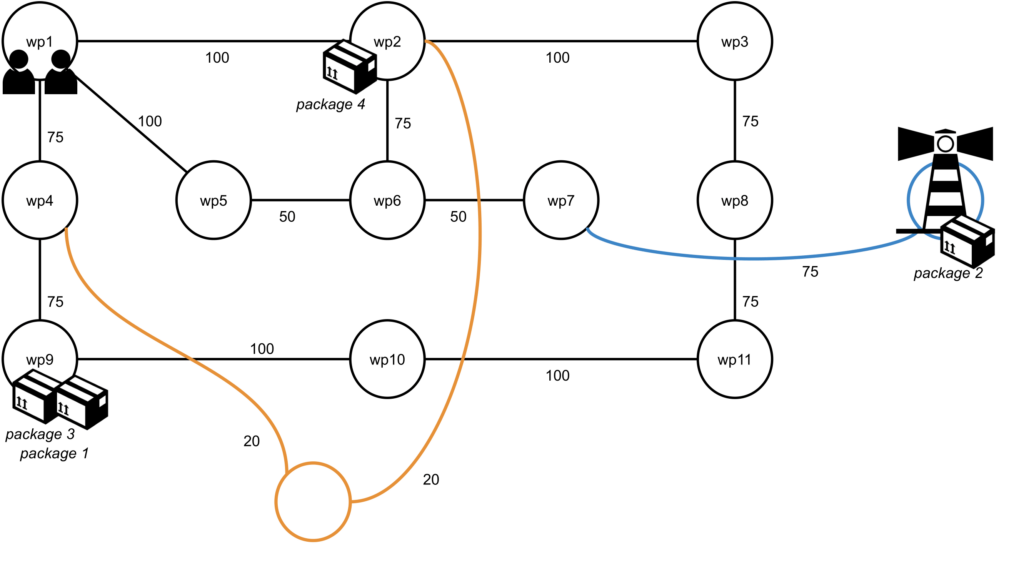
The goal must be updated to move package 2 to the lighthouse, as shown below. The final positions of the vehicles is not important.
Once it is working, you should see a timeline like this:
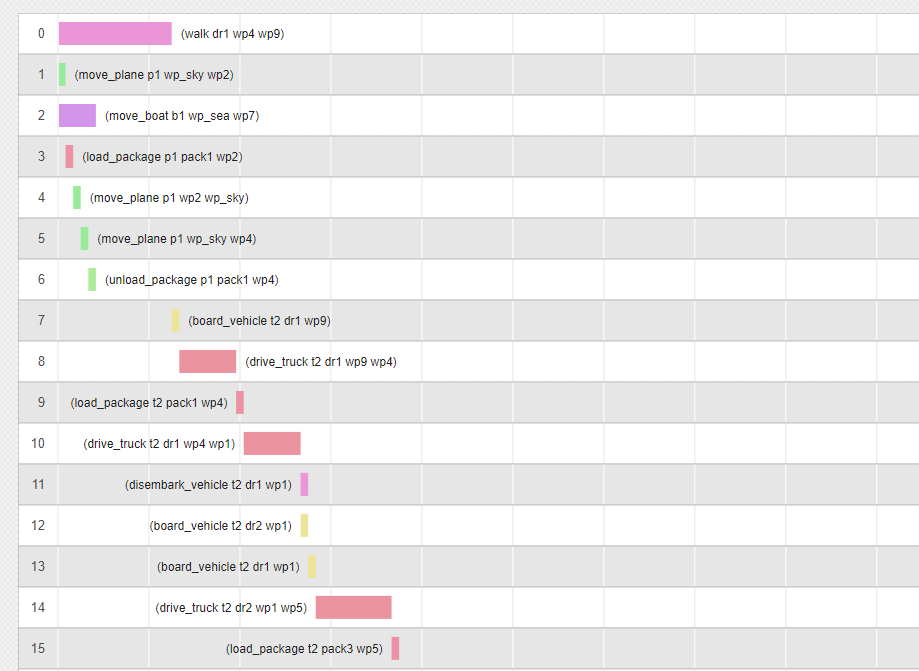
Exercise 4.3 Deadlines
Task: Add deadlines to the delivery time for each package.
A deadline can be set using a Timed Initial Literal (TIL). A TIL can be used to specify that a fact becomes true or false a set time after the initial state. In the example below, the proposition (building-open) becomes true at time 1000, and false again at time 2000.
(:init
(at 1000 (building-open))
(at 2000 (not (building-open)))- The problem (and domain) will need to be updated so that the package delivery goals must be achieved before 2500 time units.
- Experiment with different TILs to find the minimum deadline for your solution.
Exercise 4.4 Uneven Deadlines (bonus challenge)
Task: In this exercise we will use the planner to produce the solution that I prefer:
- My solution should deliver package 1 in the fastest possible time, and
- Given (1), the solution should deliver the remaining packages within the shortest possible time.
With some planners it is possible to specify an optimisation metric. For example:
(:metric minimise (delivery-time package1))However, the temporal planner connected to the online editor will only attempt to minimise total plan duration. In order to find the solution that I prefer, you will need to find a different approach and use TILs (as deadlines).
Extra Challenges
- Each truck can only make a maximum of 7 trips.
- The plane must wait a minimum of 20 time units between trips.
- Each driver must return to waypoint 1 and disembark at least once within each 400 time unit interval. This can be at the start or end of the time interval, for example at: 399, 401, 850, …
- Trucks can make any number of trips, but consume 1 unit of fuel for each time unit they are travelling. Trucks can be refuelled at stations in waypoints 3 and 9.
- Trucks also consume 0.1 fuel per time unit when they are not driving.
Note: these extra challenges may create a problem that is too difficult to solve within the time limit given to the online solver.